9 X 8 X 7

x 10 x nine x viii x 7 10 half-dozen x 5 x 4 10 3 10 2 ten 1 x' ten x' 9 x' 8 x' 6 x' 5 x' iv 10' iii x' ii x' 1 0 00 ane 01 xi 000 001 010 011 100 101 110 111 Sampling for Large Data Graham Cormode, University of Warwick G. [email protected] ac. uk Nick Duffield, Texas A&Thousand University [electronic mail protected] edu 10

Sampling for Big Data ◊ "Big" data arises in many forms: – – Physical Measurements: from science (physics, astronomy) Medical information: genetic sequences, detailed time serial Activity data: GPS location, social network action Business information: customer behavior tracking at fine detail ◊ Mutual themes: – Information is big, and growing – At that place are important patterns and trends in the data – Nosotros don't fully know where to look or how to find them

Sampling for Big Data Why Reduce? ◊ Although "big" information is most more than than just the volume… …most big information is large! ◊ Information technology is not always possible to store the data in full – Many applications (telecoms, ISPs, search engines) can't continue everything ◊ It is inconvenient to work with information in full – Just considering nosotros can, doesn't mean we should ◊ It is faster to work with a meaty summary – Better to explore data on a laptop than a cluster

Sampling for Big Data Why Sample? ◊ Sampling has an intuitive semantics – We obtain a smaller data set up with the aforementioned structure ◊ Estimating on a sample is often straightforward – Run the assay on the sample that yous would on the total data – Some rescaling/reweighting may be necessary ◊ Sampling is full general and agnostic to the assay to be washed – Other summary methods only work for certain computations – Though sampling tin can be tuned to optimize some criteria ◊ Sampling is (usually) easy to sympathize – Then prevalent that we accept an intuition about sampling

Sampling for Big Data Alternatives to Sampling ◊ Sampling is not the but game in town – Many other information reduction techniques by many names ◊ Dimensionality reduction methods – PCA, SVD, eigenvalue/eigenvector decompositions – Costly and irksome to perform on big data ◊ "Sketching" techniques for streams of data – Hash based summaries via random projections – Complex to understand limited in function ◊ Other transform/dictionary based summarization methods – Wavelets, Fourier Transform, DCT, Histograms – Not incrementally updatable, high overhead ◊ All worthy of written report – in other tutorials

Sampling for Big Data Wellness Warning: contains probabilities ◊ Will avoid detailed probability calculations, aim to requite loftier level descriptions and intuition ◊ But some probability basics are assumed – Concepts of probability, expectation, variance of random variables – Allude to concentration of measure (Exponential/Chernoff bounds) ◊ Experience free to ask questions nearly technical details along the fashion

Sampling for Big Data Outline ◊ Motivating awarding: sampling in big Internet access provider networks ◊ Basics of sampling: concepts and interpretation ◊ Stream sampling: uniform and weighted example – Variations: Curtailed sampling, sample and concord, sketch guided BREAK ◊ Advanced stream sampling: sampling as toll optimization – Var. Opt, priority, structure aware, and stable sampling ◊ Hashing and coordination – Bottom-k, consequent sampling and sketch-based sampling ◊ Graph sampling – Node, edge and subgraph sampling ◊ Decision and future directions

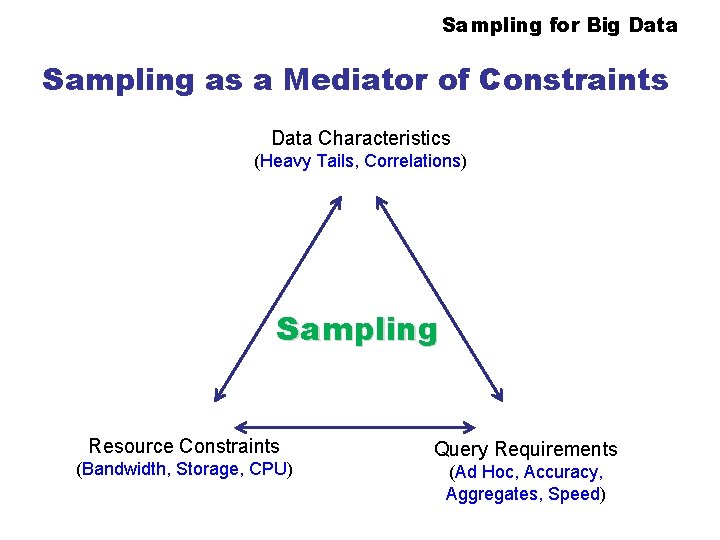
Sampling for Big Data Sampling equally a Mediator of Constraints Information Characteristics (Heavy Tails, Correlations) Sampling Resource Constraints (Bandwidth, Storage, CPU) Query Requirements (Ad Hoc, Accurateness, Aggregates, Speed)

Sampling for Big Data Motivating Application: ISP Information ◊ Will motivate many results with application to ISPs ◊ Many reasons to use such examples: – – – Expertise: tutors from telecoms earth Demand: many sampling methods developed in response to ISP needs Practice: sampling widely used in ISP monitoring, built into routers Prescience: ISPs were first to hit many "big data" problems Variety: many different places where sampling is needed ◊ Offset, a crash-course on ISP networks…

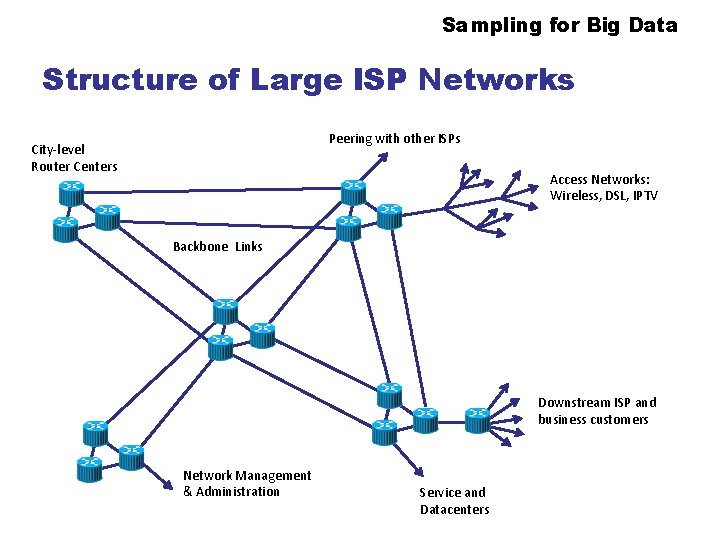
Sampling for Big Data Structure of Large ISP Networks Peering with other ISPs City-level Router Centers Access Networks: Wireless, DSL, IPTV Backbone Links Downstream ISP and business customers Network Management & Administration Service and Datacenters

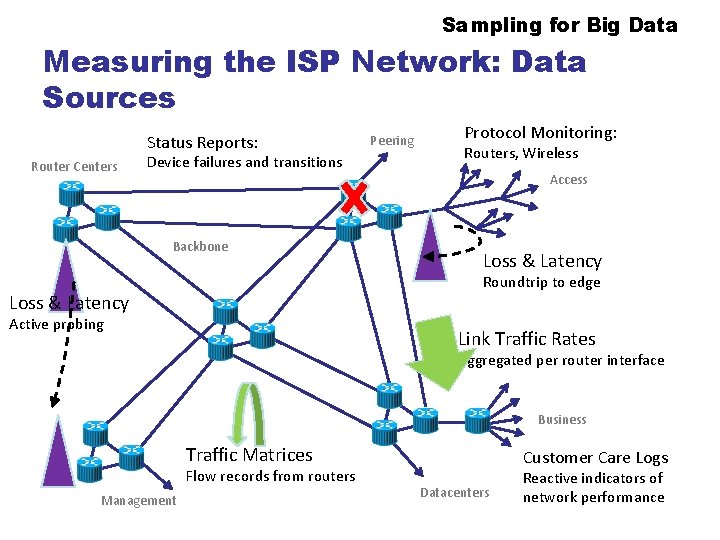
Sampling for Big Data Measuring the Internet access provider Network: Data Sources Condition Reports: Router Centers Device failures and transitions Backbone Peering Protocol Monitoring: Routers, Wireless Admission Loss & Latency Roundtrip to border Loss & Latency Active probing Link Traffic Rates Aggregated per router interface Business Traffic Matrices Flow records from routers Direction Customer Care Logs Datacenters Reactive indicators of network performance

Sampling for Big Information Why Summarize (Isp) Big Information? ◊ When manual bandwidth for measurements is limited – Non such a large issue in ISPs with in-ring collection ◊ Typically raw aggregating is non feasible (even for nation states) – High rate streaming data – Maintain historical summaries for baselining, time series analysis ◊ To facilitate fast queries – When infeasible to run exploratory queries over full data ◊ As function of hierarchical query infrastructure: – Maintain full data over limited duration window – Drill down into full data through i or more layers of summarization Sampling has been proved to be a flexible method to attain this

Sampling for Big Data Calibration: Summarization and Sampling

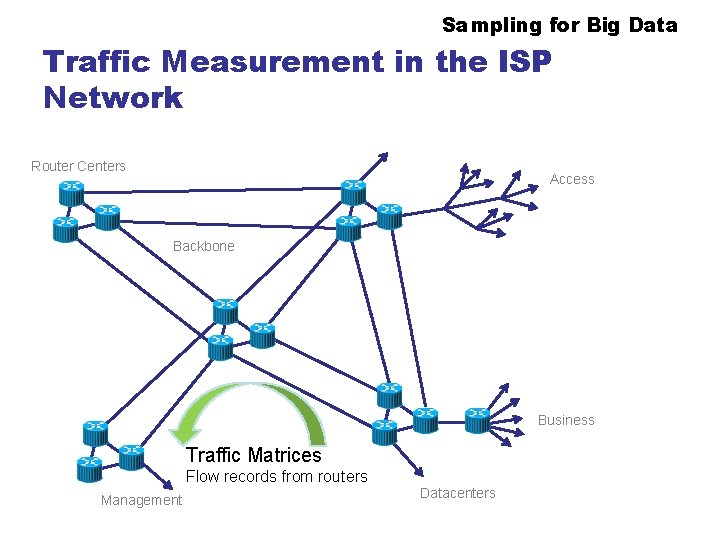
Sampling for Big Data Traffic Measurement in the Isp Network Router Centers Access Backbone Concern Traffic Matrices Flow records from routers Management Datacenters

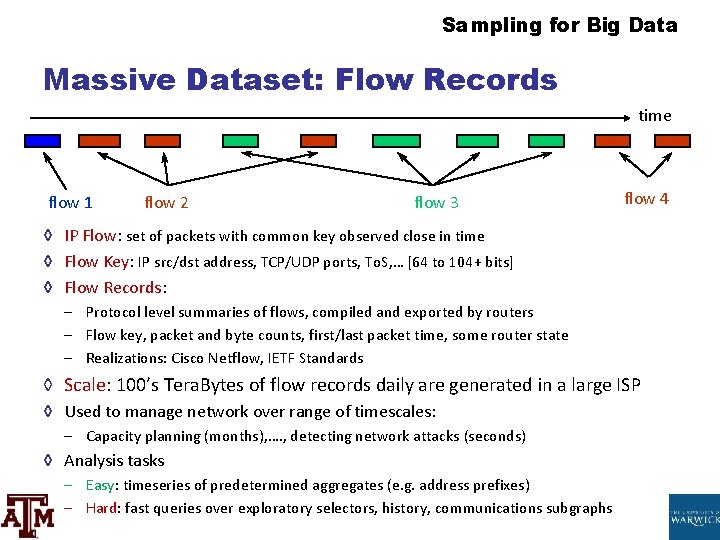
Sampling for Big Data Massive Dataset: Menses Records time menses 1 catamenia two period 3 flow 4 ◊ IP Flow: set of packets with common key observed close in fourth dimension ◊ Menstruation Fundamental: IP src/dst address, TCP/UDP ports, To. S, … [64 to 104+ bits] ◊ Flow Records: – Protocol level summaries of flows, compiled and exported by routers – Flow key, packet and byte counts, first/last package fourth dimension, some router state – Realizations: Cisco Netflow, IETF Standards ◊ Scale: 100'southward Tera. Bytes of period records daily are generated in a big ISP ◊ Used to manage network over range of timescales: – Capacity planning (months), …. , detecting network attacks (seconds) ◊ Analysis tasks – Easy: timeseries of predetermined aggregates (e. yard. address prefixes) – Hard: fast queries over exploratory selectors, history, communications subgraphs

Sampling for Big Data Flows, Flow Records and Sampling ◊ Two types of sampling used in do for internet traffic: 1. Sampling packet stream in router prior to forming flow records □ Limits the rate of lookups of packet key in catamenia cache □ Realized every bit Packet Sampled Net. Flow (more later…) 2. Downstream sampling of period records in collection infrastructure □ Limits manual bandwidth, storage requirements □ Realized in ISP measurement collection infrastructure (more later…) ◊ Two cases illustrative of general property – – Unlike underlying distributions require different sample designs Statistical optimality sometimes limited by implementation constraints □ Availability of router storage, processing cycles

Sampling for Big Data Brainchild: Keyed Data Streams ◊ Information Model: objects are keyed weights – Objects (x, k): Weight x; key k □ Instance one: objects = packets, ten = bytes, k = primal (source/destination) □ Example ii: objects = flows, x = packets or bytes, k = key □ Example three: objects = business relationship updates, 10 = credit/debit, chiliad = account ID ◊ Stream of keyed weights, {(xi , ki): i = i, 2, …, n} ◊ Generic query: subset sums – Ten(S) = Σi South eleven for S {1, ii, …, n} i. east. total weight of index subset S – Typically Southward = S(K) = {i: ki Grand} : objects with keys in K □ Case 1, 2: Ten(S(Chiliad)) = total bytes to given IP dest accost / UDP port □ Example 3: Ten(S(K)) = total balance change over set of accounts ◊ Aim: Compute fixed size summary of stream that tin can be used to estimate capricious subset sums with known fault bounds

Sampling for Big Data Inclusion Sampling and Interpretation ◊ Horvitz-Thompson Estimation: – Object of size xi sampled with probability pi – Unbiased estimate 10'i = xi / pi (if sampled), 0 if non sampled: E[x'i] = xi ◊ Linearity: – Gauge of subset sum = sum of matching estimates – Subset sum X(S)= i S xi is estimated by Ten'(S) = i S ten'i ◊ Accurateness: – Exponential Bounds: Pr[ |X'(S) - X(South)| > δX(S)] ≤ exp[-thou(δ)X(S)] – Confidence intervals: X(S) [10-( ) , 10+( )] with probability ane - ◊ Futureproof: – Don't demand to know queries at time of sampling □ "Where/where did that suspicious UDP port beginning become so agile? " □ "Which is the virtually active IP address inside than anomalous subnet? " – Retrospective estimate: subset sum over relevant keyset

Sampling for Large Data Independent Stream Sampling ◊ Bernoulli Sampling – IID sampling of objects with some probability p – Sampled weight x has HT estimate x/p ◊ Poisson Sampling – Weight xi sampled with probability pi ; HT judge xi / pi ◊ When to use Poisson vs. Bernoulli sampling? – Elephants and mice: Poisson allows probability to depend on weight… ◊ What is all-time pick of probabilities for given stream {eleven} ?

Sampling for Large Data Bernoulli Sampling ◊ The easiest possible case of sampling: all weights are 1 – Due north objects, and want to sample thou from them uniformly – Each possible subset of k should be equally likely ◊ Uniformly sample an index from N (without replacement) k times – Some subtleties: truly random numbers from [1…N] on a estimator? – Assume that random number generators are proficient enough ◊ Common trick in DB: assign a random number to each particular and sort – Costly if Due north is very large, simply and then is random access ◊ Interesting problem: take a single linear scan of data to draw sample – Streaming model of computation: meet each element in one case – Application: IP flow sampling, too many (for us) to shop – (For a while) mutual tech interview question

Sampling for Big Data Reservoir Sampling "Reservoir sampling" described past [Knuth 69, 81]; enhancements [Vitter 85] ◊ Fixed size k uniform sample from arbitrary size N stream in one pass – No need to know stream size in advance – Include start grand items west. p. 1 – Include item north > k with probability pn = one thousand/n, n > k □ Option j uniformly from {i, 2, …, north} □ If j ≤ k, bandy item northward into location j in reservoir, discard replaced item ◊ Neat proof shows the uniformity of the sampling method: – Letm. Sn(<= n) sample set up subsequently n arrivals New item: selection probability g=7 n Prob[n Sn ] = pn : = k/n Previously sampled item: induction m Sn-i westward. p. pn-1 1000 Sn due west. p. pn-1 * (one – pn / thou) = pn

Sampling for Big Data Reservoir Sampling: Skip Counting ◊ Uncomplicated approach: check each item in turn – O(1) per item: – Fine if ciphering time < interarrival time – Otherwise build up computation excess O(N) ◊ Better: "skip counting" – Find random index m(northward) of adjacent selection > northward – Distribution: Prob[m(n) ≤ k] = 1 - (1 -pn+1)*(one -pn+2)*…*(1 -pm) ◊ Expected number of selections from stream is k + Σk<grand≤N pm = k + Σk<yard≤N k/m = O(k ( ane + ln (North/k) )) ◊ Vitter' 85 provided algorithm with this average running time

Sampling for Large Information Reservoir Sampling via Society Sampling ◊ Order sampling a. k. a. bottom-k sample, min-hashing ◊ Uniform sampling of stream into reservoir of size grand ◊ Each arrival n: generate one-fourth dimension random value rn U[0, 1] – rn besides known as hash, rank, tag… ◊ Store k items with the smallest random tags 0. 391 n due north n 0. 908 0. 291 0. 555 0. 619 0. 273 Each item has aforementioned chance of to the lowest degree tag, then uniform Fast to implement via priority queue Can run on multiple input streams separately, then merge

Sampling for Big Data Treatment Weights ◊ And so far: uniform sampling from a stream using a reservoir ◊ Extend to non-uniform sampling from weighted streams – Easy case: grand=1 – Sampling probability p(northward) = xn/Wn where Wn = i=1 n eleven ◊ k>i is harder – Tin accept elements with large weight: would be sampled with prob 1? ◊ Number of different weighted gild-sampling schemes proposed to realize desired distributional objectives – – – Rank rn = f(un, xn ) for some part f and un U[0, one] grand-mins sketches [Cohen 1997], Lesser-m sketches [Cohen Kaplan 2007] [Rosen 1972], Weighted random sampling [Efraimidis Spirakis 2006] Order PPS Sampling [Ohlsson 1990, Rosen 1997] Priority Sampling [Duffield Lund Thorup 2004], [Alon+DLT 2005]

Sampling for Big Data Weighted random sampling ◊ Weighted random sampling [Efraimidis Spirakis 06] generalizes minwise – – For each item draw rn uniformly at random in range [0, one] Compute the 'tag' of an item as rn (i/xn) Keep the items with the one thousand smallest tags Can prove the correctness of the exponential sampling distribution ◊ Can also brand efficient via skip counting ideas

Sampling for Large Information Priority Sampling ◊ Each detail xi given priority zi = xi / ri with rn compatible random in (0, 1] ◊ Maintain reservoir of one thousand+1 items (xi , zi ) of highest priority ◊ Estimation – Let z* = (one thousand+1)st highest priority – Summit-m priority items: weight estimate ten'I = max{ xi , z* } – All other items: weight guess zero ◊ Statistics and premises – x'I unbiased; cipher covariance: Cov[x'i , x'j ] = 0 for i≠j – Relative variance for any subset sum ≤ one/(m-1) [Szegedy, 2006]

Sampling for Big Data Priority Sampling in Databases ◊ One Time Sample Grooming – Compute priorities of all items, sort in decreasing priority order □ No discard ◊ Sample and Estimate – Judge whatever subset sum X(S) = i S eleven by X'(S) = i S x'I for some S' S – Method: select items in decreasing priority order ◊ Two variants: bounded variance or complexity 1. S' = first yard items from S: relative variance bounded ≤ one/(g-1) □ x'I = max{ xi , z* } where z* = (k+1)st highest priority in Due south ii. South' = items from Southward in showtime m: execution time O(k) □ 10'I = max{ 11 , z* } where z* = (k+1)st highest priority [Alon et. al. , 2005]

Sampling for Big Information Making Stream Samples Smarter ◊ Observation: we see the whole stream, even if we can't store it – Can keep more than information nearly sampled items if repeated – Unproblematic information: if detail sampled, count all repeats ◊ Counting Samples [Gibbons & Mattias 98] – Sample new items with fixed probability p, count repeats every bit ci – Unbiased guess of total count: 1/p + (ci – 1) ◊ Sample and Concur [Estan & Varghese 02]: generalize to weighted keys – New cardinal with weight b sampled with probability 1 - (one -p)b ◊ Lower variance compared with contained sampling – But sample size will grow as pn ◊ Adaptive sample and hold: reduce p when needed – "Sticky sampling": geometric decreases in p [Manku, Motwani 02] – Much subsequent work tuning subtract in p to maintain sample size

Sampling for Big Data Sketch Guided Sampling ◊ Go further: avoid sampling the heavy keys as much – Compatible sampling will option from the heavy keys over again and once again ◊ Idea: utilize an oracle to tell when a key is heavy [Kumar Xu 06] – Arrange sampling probability accordingly ◊ Can use a "sketch" information structure to play the part of oracle – Like a hash table with collisions, tracks approximate frequencies – Due east. g. (Counting) Flower Filters, Count-Min Sketch ◊ Track probability with which key is sampled, utilise HT estimators – Fix probability of sampling cardinal with (estimated) weight due west equally 1/(1 + w) for parameter : decreases every bit west increases – Decreasing improves accuracy, increases sample size

Sampling for Big Data Challenges for Smart Stream Sampling ◊ Current router constraints – Catamenia tables maintained in fast expensive SRAM □ To back up per packet key lookup at line charge per unit ◊ Implementation requirements – Sample and Hold: still need per package lookup – Sampled Net. Flow: (compatible) sampling reduces lookup rate □ Easier to implement despite inferior statistical properties ◊ Long development times to realize new sampling algorithms ◊ Similar concerns touch on sampling in other applications – Processing large amounts of information needs awareness of hardware – Compatible sampling ways no coordination needed in distributed setting

Sampling for Large Data Time to come for Smarter Stream Sampling ◊ Software Defined Networking – Current: proprietary software running on special vendor equipment – Future: open software and protocols on commodity hardware ◊ Potentially offers flexibility in traffic measurement – Allocate organization resources to measurement tasks as needed – Dynamic reconfiguration, fine grained tuning of sampling – Stateful package inspection and sampling for network security ◊ Technical challenges: – High rate packet processing in software – Transparent support from commodity hardware – Open up. Sketch: [Yu, Jose, Miao, 2013] ◊ Aforementioned issues in other applications: use of commodity programmable HW

Sampling for Large Information Stream Sampling: Sampling as Cost Optimization

Sampling for Big Information Matching Data to Sampling Assay ◊ Generic problem 1: Counting objects: weight eleven = one Bernoulli (uniform) sampling with probability p works fine – Estimated subset count X'(Southward) = #{samples in South} / p – Relative Variance (X'(South)) = (one/p -one)/X(Southward) □ given p, get any desired accurateness for large enough South ◊ Generic trouble ii: xi in Pareto distribution, a. k. a. 80 -20 law – Small proportion of objects possess a big proportion of total weight □ How to best to sample objects to accurately judge weight? – Uniform sampling? □ probable to omit heavy objects big hitting on accuracy □ making selection set Due south big doesn't assistance – Select m largest objects ? □ biased & smaller objects systematically ignored

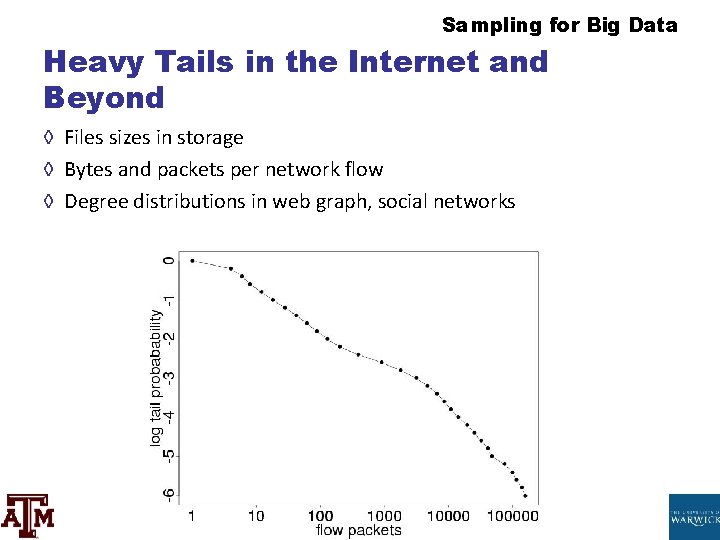
Sampling for Large Data Heavy Tails in the Internet and Beyond ◊ Files sizes in storage ◊ Bytes and packets per network flow ◊ Degree distributions in web graph, social networks

Sampling for Big Data Non-Compatible Sampling ◊ Extensive literature: see book by [Tille, "Sampling Algorithms", 2006] ◊ Predates "Big Data" – Focus on statistical properties, not so much computational ◊ IPPS: Inclusion Probability Proportional to Size – Variance Optimal for HT Estimation – Sampling probabilities for multivariate version: [Chao 1982, Tille 1996] – Efficient stream sampling algorithm: [Cohen et. al. 2009]

Sampling for Big Data Costs of Non-Compatible Sampling ◊ Independent sampling from n objects with weights {x 1, … , xn} ◊ Goal: notice the "best" sampling probabilities {p 1, … , pn} ◊ Horvitz-Thompson: unbiased interpretation of each xi by ◊ Ii costs to balance: 1. Estimation Variance: Var(x'i) = 10 two i (ane/pi – 1) two. Expected Sample Size: ipi ◊ Minimize Linear Combination Cost: i (xi 2(1/pi – 1) + z 2 pi) – z expresses relative importance of small sample vs. modest variance

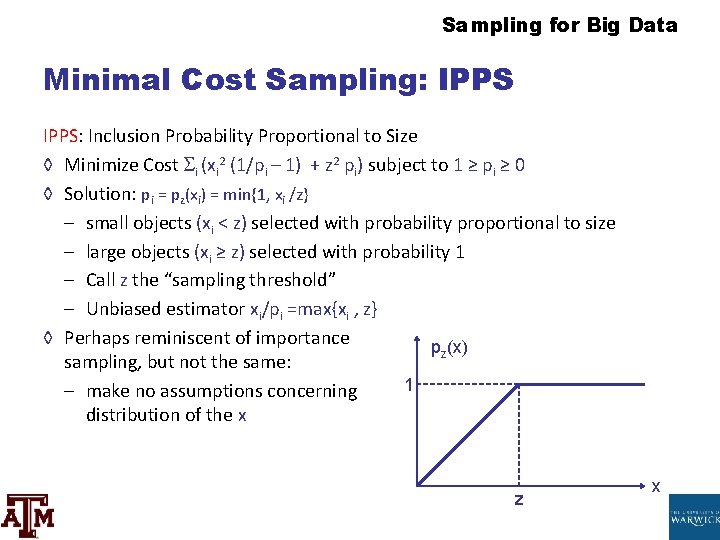
Sampling for Large Data Minimal Cost Sampling: IPPS: Inclusion Probability Proportional to Size ◊ Minimize Cost i (11 2 (1/pi – one) + z 2 pi) subject field to 1 ≥ pi ≥ 0 ◊ Solution: pi = pz(xi) = min{1, xi /z} – minor objects (xi < z) selected with probability proportional to size – large objects (xi ≥ z) selected with probability 1 – Call z the "sampling threshold" – Unbiased estimator xi/pi =max{xi , z} ◊ Perhaps reminiscent of importance pz(x) sampling, but not the same: 1 – make no assumptions concerning distribution of the ten z x

Sampling for Big Data Mistake Estimates and Bounds ◊ Variance Based: – HT sampling variance for unmarried object of weight xi □ Var(x'i) = x 2 i (1/pi – 1) = x 2 i (1/min{ane, xi/z} – ane) ≤ z eleven – Subset sum X(Due south)= i S eleven is estimated past X'(S) = i Southward x'i □ Var(Ten'(Due south)) ≤ z Ten(S) ◊ Exponential Bounds – East. one thousand. Prob[X'(S) = 0] ≤ exp(- 10(S) / z ) ◊ Premises are simple and powerful – depend only on subset sum X(Southward), not individual constituents

Sampling for Large Data Sampled IP Traffic Measurements ◊ Package Sampled Net. Menstruation – Sample packet stream in router to limit charge per unit of fundamental lookup: compatible 1/N – Aggregate sampled packets into period records by fundamental ◊ Model: packet stream of (key, bytesize) pairs { (bi, ki) } ◊ Packet sampled flow record (b, k) where b = Σ {bi : i sampled ∧ ki = k} – HT estimate b*North of total bytes in flow ◊ Downstream sampling of flow records in measurement infrastructure – IPPS sampling, probability min{one, b*N/z} ◊ Chained variance leap for any subset sum X of flows – Var(X') ≤ (z + Nbmax) X where bmax = maximum packet byte size – Regardless of how packets are distributed amidst flows [Duffield, Lund, Thorup, IEEE To. It, 2004]

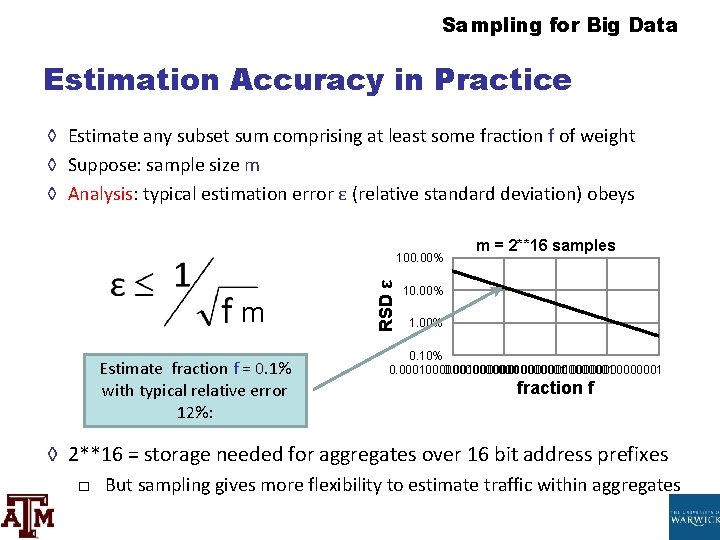
Sampling for Big Data Estimation Accuracy in Practice ◊ Estimate any subset sum comprising at least some fraction f of weight ◊ Suppose: sample size m ◊ Analysis: typical interpretation error ε (relative standard deviation) obeys thou Estimate fraction f = 0. 1% with typical relative error 12%: RSD ε 100. 00% yard = 2**xvi samples 10. 00% 1. 00% 0. ten% 0. 000100000000000001 0. 0100000001 0. 100000001 fraction f ◊ ii**16 = storage needed for aggregates over 16 bit accost prefixes □ Merely sampling gives more than flexibility to guess traffic inside aggregates

Sampling for Big Data Heavy Hitters: Exact vs. Aggregate vs. Sampled ◊ Sampling does not tell you where the interesting features are – Only does speed up the power to find them with existing tools ◊ Example: Heavy Hitter Detection – Setting: Flow records reporting 10 GB/due south traffic stream – Aim: find Heavy Hitters = IP prefixes comprising ≥ 0. 1% of traffic – Response time needed: five infinitesimal ◊ Compare: – Exact: ten GB/s x five minutes yields up of 300 M catamenia records – 64 k aggregates over xvi bit prefixes: no deeper drill-down possible – Sampled: 64 k flow records: whatever aggregate ≥ 0. 1% accurate to 10% Exact Aggregate Sampled

Sampling for Big Data Cost Optimization for Sampling Several different approaches optimize for unlike objectives: 1. Fixed Sample Size IPPS Sample – Variance Optimal sampling: minimal variance unbiased interpretation 2. Structure Enlightened Sampling – Better estimation accurateness for subnet queries using topological cost three. Fair Sampling – Adaptively residue sampling budget over subpopulations of flows – Uniform estimation accuracy regardless of subpopulation size 4. Stable Sampling – Increase stability of sample fix by imposing toll on changes

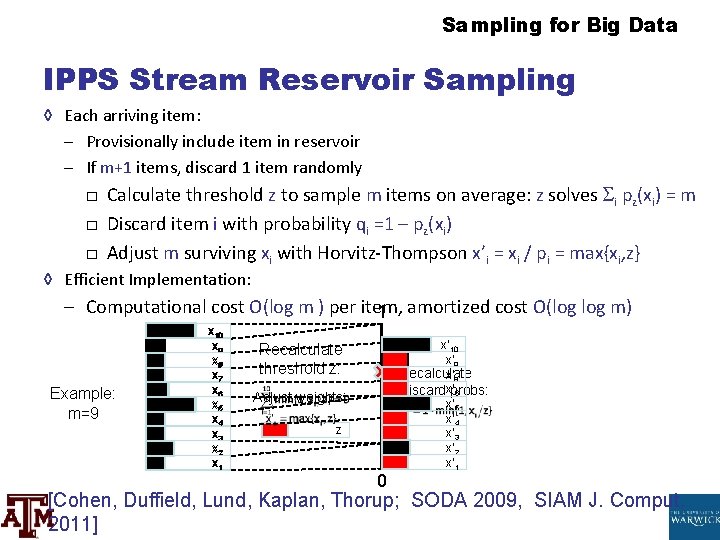
Sampling for Big Data IPPS Stream Reservoir Sampling ◊ Each arriving item: – Provisionally include item in reservoir – If 1000+1 items, discard 1 item randomly □ Calculate threshold z to sample m items on average: z solves i pz(11) = m □ Discard item i with probability qi =1 – pz(eleven) □ Adjust m surviving xi with Horvitz-Thompson x'i = xi / pi = max{eleven, z} ◊ Efficient Implementation: – Computational price O(log m ) per item, one amortized cost O(log m) Example: m=9 x 10 10 ix x 8 x 7 ten 6 10 five x 4 10 3 x two x 1 Recalculate threshold z: Suit weights: z 0 x' 10 10' ix Recalculate x' 8 Discardx'probs: six x' 5 x' 4 x' 3 x' 2 ten' 1 [Cohen, Duffield, Lund, Kaplan, Thorup; SODA 2009, SIAM J. Comput. 2011]

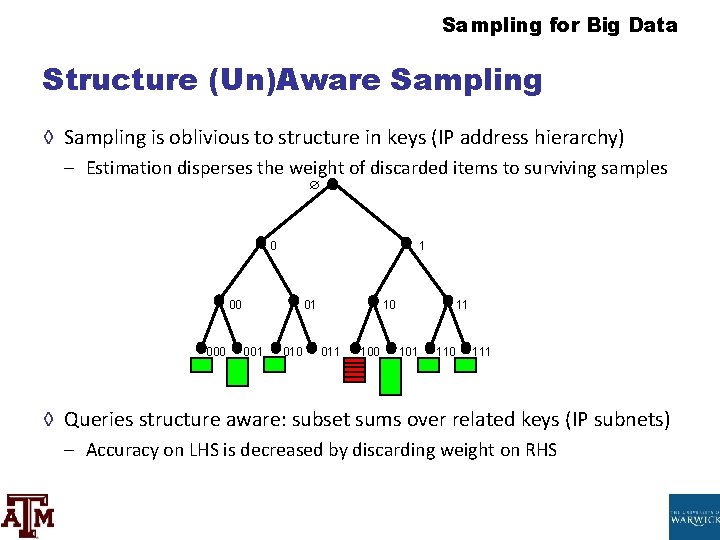
Sampling for Big Data Construction (Un)Aware Sampling ◊ Sampling is oblivious to structure in keys (IP address hierarchy) – Interpretation disperses the weight of discarded items to surviving samples 0 one 00 01 001 010 10 011 100 11 101 110 111 ◊ Queries construction aware: subset sums over related keys (IP subnets) – Accuracy on LHS is decreased past discarding weight on RHS

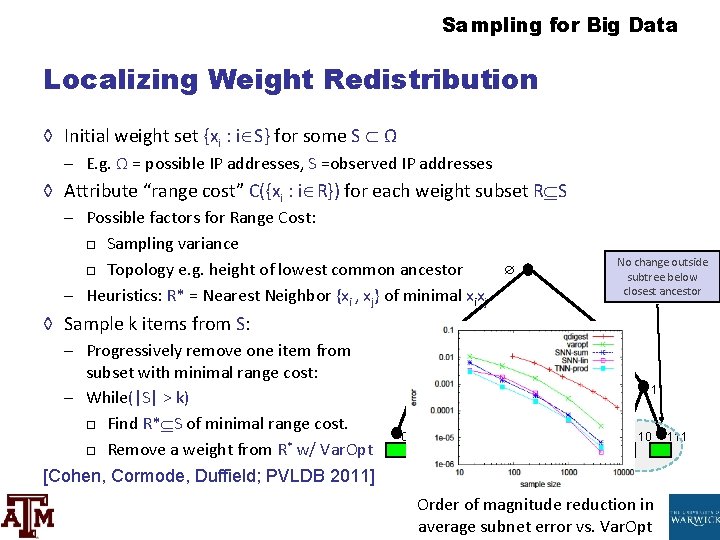
Sampling for Big Data Localizing Weight Redistribution ◊ Initial weight set {xi : i S} for some Due south Ω – Eastward. g. Ω = possible IP addresses, South =observed IP addresses ◊ Attribute "range cost" C({xi : i R}) for each weight subset R S – Possible factors for Range Toll: □ Sampling variance □ Topology e. g. summit of lowest common ancestor – Heuristics: R* = Nearest Neighbor {xi , xj} of minimal xixj ◊ Sample chiliad items from South: – Progressively remove 1 particular from subset with minimal range cost: – While(|S| > one thousand) □ Notice R* South of minimal range cost. □ Remove a weight from R* w/ Var. Opt [Cohen, Cormode, Duffield; PVLDB 2011] No modify outside subtree below closest ancestor 0 1 00 01 001 010 ten 011 100 11 101 110 Order of magnitude reduction in average subnet error vs. Var. Opt 111

Sampling for Large Data Fair Sampling Across Subpopulations ◊ Assay queries frequently focus on specific subpopulations – E. g. networking: unlike customers, user applications, network paths ◊ Wide variation in subpopulation size – 5 orders of magnitude variation in traffic on interfaces of access router ◊ If compatible sampling across subpopulations: – Poor estimation accurateness on subset sums within small subpopulations Colour = subpopulation , Sample = interesting items – occurrence proportional to subpopulation size Uniform Sampling across subpopulations: – Difficult to track proportion of interesting items inside pocket-size subpopulations:

Sampling for Big Information Fair Sampling Across Subpopulations ◊ Minimize relative variance past sharing budget m over subpopulations – Full due north objects in subpopulations northward ane, …, nd with ini=n – Allocate budget mi to each subpopulation ni with imi=1000 ◊ Minimize boilerplate population relative variance R = const. i 1/mi ◊ Theorem: – R minimized when {mi} are Max-Min Fair share of m under demands {ni} ◊ Streaming – Problem: don't know subpopulation sizes {ni} in advance ◊ Solution: progressive fair sharing as reservoir sample – Provisionally include each arrival – Discard 1 item every bit Var. Opt sample from any maximal subpopulation ◊ Theorem [Duffield; Sigmetrics 2012]: – Max-Min Fair at all times; equality in distribution with Var. Opt samples {mi from ni}

Sampling for Big Data Stable Sampling ◊ Setting: Sampling a population over successive periods ◊ Sample independently at each time period? – Cost associated with sample churn – Time serial analysis of set of relatively stable keys ◊ Find sampling probabilities through cost minimization – Minimize Toll = Interpretation Variance + z * E[#Churn] ◊ Size m sample with maximal expected churn D – weights {xi}, previous sampling probabilities {pi} – notice new sampling probabilities {qi} to minimize cost of taking m samples – Minimize nine 2 i / qi subject to ane ≥ qi ≥ 0, I qi = m and I | pi – qi | ≤ D [Cohen, Cormode, Duffield, Lund 13]

Sampling for Big Data Summary of Part one ◊ Sampling as a powerful, full general summarization technique ◊ Unbiased estimation via Horvitz-Thompson estimators ◊ Sampling from streams of data – Compatible sampling: reservoir sampling – Weighted generalizations: sample and hold, counting samples ◊ Advances in stream sampling – The cost principle for sample design, and IPPS methods – Threshold, priority and Var. Opt sampling – Extending the toll principle: □ structure aware, fair sampling, stable sampling, sketch guided

Sampling for Big Information Outline ◊ Motivating application: sampling in large Isp networks ◊ Basics of sampling: concepts and interpretation ◊ Stream sampling: compatible and weighted case – Variations: Concise sampling, sample and hold, sketch guided Interruption ◊ Advanced stream sampling: sampling as cost optimization – Var. Opt, priority, construction enlightened, and stable sampling ◊ Hashing and coordination – Lesser-k, consequent sampling and sketch-based sampling ◊ Graph sampling – Node, border and subgraph sampling ◊ Determination and time to come directions

Sampling for Large Information Scale: Hashing and Coordination

Sampling for Big Information Sampling from the ready of items ◊ Sometimes demand to sample from the distinct fix of objects – Not influenced by the weight or number of occurrences – E. m. sample from the singled-out ready of flows, regardless of weight ◊ Need sampling method that is invariant to duplicates ◊ Basic idea: build a role to decide what to sample – A "random" function f(k) R – Utilize f(thousand) to make a sampling determination: consistent decision for same key

Sampling for Big Information Permanent Random Numbers ◊ Ofttimes user-friendly to remember of f equally giving "permanent random numbers" – Permanent: assigned once and for all – Random: care for every bit if fully randomly chosen ◊ The permanent random number is used in multiple sampling steps – Aforementioned "random" number each fourth dimension, so consistent (correlated) decisions ◊ Example: utilise PRNs to draw a sample of s from Northward via order sampling – If s << N, minor run a risk of seeing same element in dissimilar samples – Via PRN, stronger take chances of seeing same element □ Tin track properties over fourth dimension, gives a class of stability ◊ Easiest way to generate PRNs: apply a hash function to the element id – Ensures PRN tin be generated with minimal coordination – Explicitly storing a random number for all observed keys does not scale

Sampling for Big Data Hash Functions Many possible choices of hashing functions: ◊ Cryptographic hash functions: SHA-1, Medico 5, etc. – Results announced "random" for most tests (using seed/salt) – Can be slow for high speed/high volume applications – Total power of cryptographic security not needed for about statistical purposes □ Although possible some trade-offs in robustness to subversion if not used ◊ Heuristic hash functions: srand(), mod – Commonly pretty fast – May not be random enough: structure in keys may cause collisions ◊ Mathematical hash functions: universal hashing, chiliad-wise hashing – Accept precise mathematical properties on probabilities – Tin be implemented to be very fast

Sampling for Big Data Mathematical Hashing ◊ Grand-wise independence: Pr[h(x i) = y 1 h(x ii) = y 2 … h(xt) = yt] = one/Rt – Simple part: ctxt + ct-1 xt-1 + … c 1 ten + c 0 mod P – For fixed prime P, randomly chosen c 0 … ct – Can be made very fast (choose P to be Mersenne prime to simplify mods) ◊ (Twisted) tabulation hashing [Thorup Patrascu 13] – – – Interpret each cardinal as a sequence of brusk characters, e. k. 8 * 8 bits Use a "truly random" look-upwardly table for each character (and then 8 * 256 entries) Take the sectional-OR of the relevant table values Fast, and fairly compact Strong enough for many applications of hashing (hash tables etc. )

Sampling for Big Data Lesser-thou sampling 0. 391 0. 908 0. 291 0. 391 0. 273 ◊ Sample from the set of distinct keys – Hash each key using appropriate hash part – Continue information on the keys with the southward smallest hash values – Think of equally guild sampling with PRNs… ◊ Useful for estimating backdrop of the support gear up of keys – Evaluate any predicate on the sampled set of keys ◊ Same concept, several different names: – Bottom-k sampling, Min-wise hashing, K-minimum values

Sampling for Big Data Subset Size Interpretation from Bottom-k ◊ Want to gauge the fraction t = |A|/|D| – D is the observed set of information – A is an arbitrary subset given later – E. thou. fraction of customers who are sports fans from midwest aged eighteen -35 ◊ Simple algorithm: – Run lesser-k to become sample set S, estimate t' = |A ∩ S|/south – Fault decreases as one/√s – Analysis due to [Thorup 13]: simple hash functions suffice for big enough southward

Sampling for Big Data Similarity Estimation ◊ How similar are two sets, A and B? ◊ Jaccard coefficient: |A B|/|A B| – ane if A, B identical, 0 if they are disjoint – Widely used, e. 1000. to measure document similarity ◊ Elementary approach: sample an detail uniformly from A and B – Probability of seeing aforementioned item from both: |A B|/(|A| |B|) – Chance of seeing aforementioned item too depression to exist informative ◊ Coordinated sampling: use same hash office to sample from A, B – Probability that same detail sampled: |A B|/|A B| – Echo: the average number of agreements gives Jaccard coefficient – Concentration: (condiment) error scales every bit 1/√s

Sampling for Large Data Technical Issue: Min-wise hashing ◊ For analysis to work, the hash role must exist fully random – All possibly permutations of the input are equally likely – Unrealistic in practice: description of such a function is huge ◊ "Simple" hash functions don't work well – Universal hash functions are too skewed ◊ Need hash functions that are "approximately min-wise" – Probability of sampling a subset is well-nigh uniform – Tabulation hashing a simple mode to reach this

Sampling for Big Data Bottom-yard hashing for F 0 Estimation ◊ F 0 is the number of distinct items in the stream – a fundamental quantity with many applications – E. grand. number of singled-out flows seen on a backbone link ◊ Let m exist the domain of stream elements: each data item is [1…g] ◊ Pick a random (pairwise) hash part h: [m] [R] 0 R ◊ Employ lesser-m sampling under hash function h vs R – Permit vs = s'th smallest (distinct) value of h(i) seen ◊ If north = F 0 < s, give exact answer, else estimate F' 0 = s. R/vs – vs/R fraction of hash domain occupied by s smallest

Sampling for Big Data Analysis of F 0 algorithm ◊ Tin can evidence that it is unlikely to have an overestimate – Besides many items hashed beneath a fixed value – Can care for each event of an item hashing too low as independent ◊ Similar outline to prove unlikely to have an overestimate ◊ (Relative) error scales every bit 1/√s ◊ Space price: – Store south hash values, so O(s log m) bits – Can meliorate to O(s + log m) with additional hashing tricks – Run across too "Streamed Gauge Counting of Distinct Elements", KDD' 14 0 R vs s. R/(1+ )n R

Sampling for Big Data Consistent Weighted Sampling ◊ Desire to extend bottom-grand results when data has weights ◊ Specifically, two data sets A and B where each element has weight – Weights are aggregated: we see whole weight of element together ◊ Weighted Jaccard: desire probability that aforementioned key is called by both to be i min(A(i), B(i))/ i max(A(i), B(i)) ◊ Sampling method should obey uniformity and consistency – Uniformity: element i picked from A with probability proportional to A(i) – Consistency: if i is picked from A, and B(i) > A(i), then i also picked for B ◊ Simple solution: assuming integer weights, care for weight A(i) as A(i) unique (different) copies of element i, apply bottom-k – Limitations: slow, unscalable when weights can exist big – Demand to rescale fractional weights to integral multiples

Sampling for Big Information Consequent Weighted Sampling ◊ Efficient sampling distributions exist achieving uniformity and consistency ◊ Basic idea: consider a weight w as westward/ different elements – Compute the probability that any of these achieves the minimum value – Study the limiting distribution as 0 ◊ Consistent Weighted Sampling [Manasse, Mc. Sherry, Talway 07], [Ioffe 10] – Utilize hash of item to determine which points sampled via careful transform – Many details needed to incorporate bit-precision, allow fast computation ◊ Other combinations of cardinal weights are possible [Cohen Kaplan Sen 09] – Min of weights, max of weights, sum of (accented) differences

Sampling for Big Data Trajectory Sampling ◊ Aims [Duffield Grossglauser 01]: – Probe packets at each router they traverse – Collate reports to infer link loss and latency – Need to sample; independent sampling no use ◊ Hash-based sampling: – – All routers/packets: compute hash h of invariant packet fields Sample if h some H and report to collector; tune sample rate with |H| Use high entropy packet fields as hash input, east. g. IP addresses, ID field Hash function selection trade-off betwixt speed, uniformity & security ◊ Standardized in Internet Engineering Job Force (IETF) – Service providers demand consistency across different vendors – Several hash functions standardized, extensible – Same issues arise in other big information ecosystems (apps and APIs)

Sampling for Big Data Hash Sampling in Network Management ◊ Many different network subsystems used to provide service – Monitored through event logs, passive measurement of traffic & protocols – Need cross-system sample that captures full interaction between network and a representative set of users ◊ Platonic: hash-based selection based on common identifier ◊ Administrative challenges! Organizational diversity ◊ Timeliness claiming: – Selection identifier may not be present at a measurement location – Case: common identifier = anonymized customer id □ Passive traffic measurement based on IP address □ Mapping of IP address to customer ID not available remotely □ Attribution of traffic IP address to a user difficult to compute at line speed

Sampling for Big Information Advanced Sampling from Sketches ◊ Difficult case: inputs with positive and negative weights ◊ Want to sample based on the overall frequency distribution – Sample from support ready of northward possible items – Sample proportional to (absolute) total weights – Sample proportional to some function of weights ◊ How to practise this sampling effectively? – Challenge: may be many elements with positive and negative weights – Amass weights may end upwards goose egg: how to find the non-zip weights? ◊ Contempo approach: 50 0 sampling – Fifty 0 sampling enables novel "graph sketching" techniques – Sketches for connectivity, sparsifiers [Ahn, Guha, Mc. Gregor 12]

Sampling for Big Data Fifty 0 Sampling ◊ L 0 sampling: sample with prob ≈ fi 0/F 0 – i. e. , sample (about) uniformly from items with not-zero frequency ◊ Full general approach: [Frahling, Indyk, Sohler 05, C. , Muthu, Rozenbaum 05] – Sub-sample all items (present or not) with probability p – Generate a sub-sampled vector of frequencies fp – Feed fp to a k-thin recovery data structure □ Allows reconstruction of fp if F 0 < k – If fp is k-sparse, sample from reconstructed vector – Echo in parallel for exponentially shrinking values of p

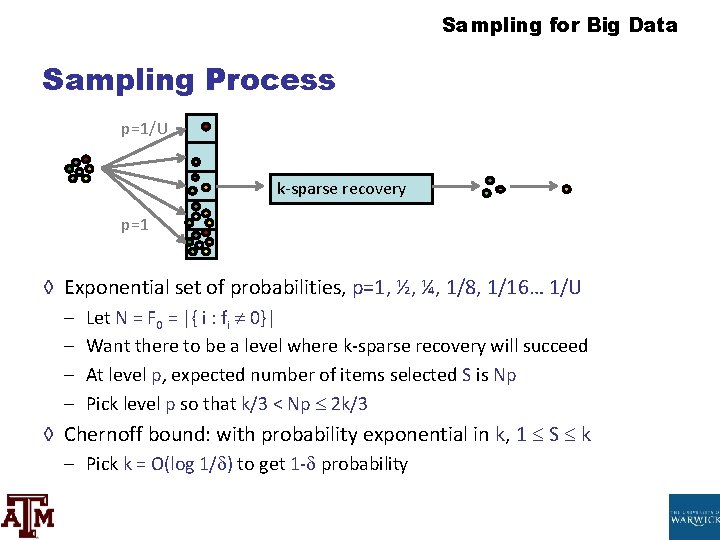
Sampling for Large Data Sampling Procedure p=1/U k-thin recovery p=1 ◊ Exponential set up of probabilities, p=1, ½, ¼, i/8, one/16… 1/U – – Permit N = F 0 = |{ i : fi 0}| Want there to be a level where k-sparse recovery will succeed At level p, expected number of items selected Due south is Np Pick level p so that k/iii < Np 2 k/3 ◊ Chernoff spring: with probability exponential in one thousand, 1 S grand – Pick k = O(log i/ ) to become 1 - probability

Sampling for Big Data Hash-based sampling summary ◊ Use hash functions for sampling where some consistency is needed – Consistency over repeated keys – Consistency over distributed observations ◊ Hash functions accept duality of random and fixed – Treat as random for statistical analysis – Care for as stock-still for giving consistency properties ◊ Can become quite complex and subtle – Complex sampling distributions for consequent weighted sampling – Tricky combination of algorithms for Fifty 0 sampling ◊ Plenty of scope for new hashing-based sampling methods

Sampling for Big Data Scale: Massive Graph Sampling

Sampling for Big Data Massive Graph Sampling ◊ "Graph Service Providers" – Search providers: web graphs (billions of pages indexed) – Online social networks □ Facebook: ~109 users (nodes), ~1012 links – ISPs: communications graphs □ From flow records: node = src or dst IP, border if traffic flows between them ◊ Graph service provider perspective – Already accept all the data, only how to utilize it? – Want a general purpose sample that can: □ Quickly provide answers to exploratory queries □ Compactly annal snapshots for retrospective queries & baselining ◊ Graph consumer perspective – Desire to obtain a realistic subgraph directly or via crawling/API

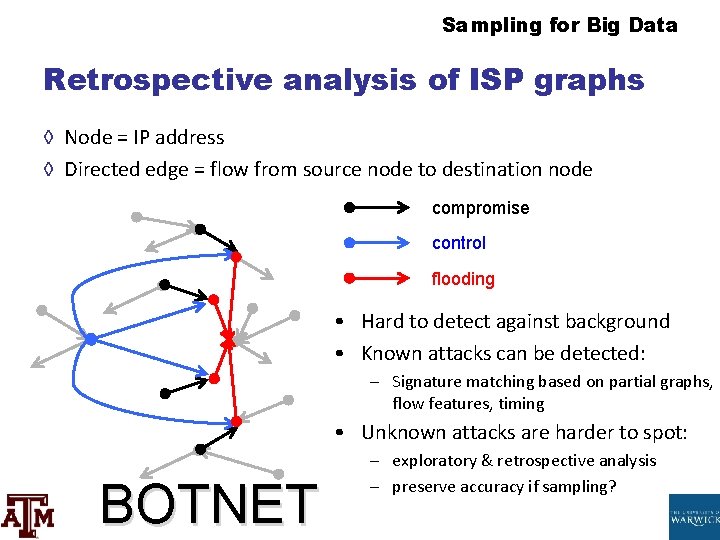
Sampling for Big Data Retrospective analysis of Internet service provider graphs ◊ Node = IP accost ◊ Directed edge = flow from source node to destination node compromise control flooding • Difficult to detect against background • Known attacks tin be detected: – Signature matching based on partial graphs, menses features, timing • Unknown attacks are harder to spot: BOTNET – exploratory & retrospective analysis – preserve accuracy if sampling?

Sampling for Big Data Goals for Graph Sampling Crudely split up into three classes of goal: one. Written report local (node or edge) backdrop – Boilerplate of users (nodes), average length of conversation (edges) ii. Approximate global properties or parameters of the network – Average caste, shortest path distribution 3. Sample a "representative" subgraph – Test new algorithms and learning more chop-chop than on full graph ◊ Challenges: what backdrop should the sample preserve? – The notion of "representative" is very subjective – Can list backdrop that should exist preserved (e. one thousand. degree dbn, path length dbn), but at that place always more…

Sampling for Large Data Models for Graph Sampling Many possible models, only reduce to two for simplicity (run into tutorial by Hasan, Ahmed, Neville, Kompella in KDD 13) ◊ Static model: full access to the graph to draw the sample – The (massive) graph is attainable in full to make the small sample ◊ Streaming model: edges arrive in some arbitrary order – Must make sampling decisions on the fly ◊ Other graph models capture dissimilar admission scenarios – Itch model: e. g. exploring the (deep) web, API gives node neighbours – Adjacency list streaming: see all neighbours of a node together

Sampling for Big Data Node and Edge Backdrop ◊ Gross over-generalization: node and edge properties tin be solved using previous techniques – Sample nodes/edge (in a stream) – Handle duplicates (aforementioned border many times) via hash-based sampling – Track backdrop of sampled elements □ Due east. g. count the degree of sampled nodes ◊ Some challenges. E. g. how to sample a node proportional to its caste? – If degree is known (precomputed), then use these as weights – Else, sample edges uniformly, then sample each finish with probability ½

Sampling for Big Information Induced subgraph sampling ◊ Node-induced subgraph – – Pass 1: Sample a set of nodes (eastward. one thousand. uniformly) Pass two: collect all edges incident on sampled nodes Can collapse into a single streaming pass Tin't know in advance how many edges will be sampled ◊ Edge-induced subgraph – Sample a fix of edges (e. k. uniformly in one laissez passer) – Resulting graph tends to be sparse, asunder ◊ Border-induced variant [Ahmed Neville Kompella 13]: – Have 2d pass to fill in edges on sampled nodes – Hack: combine passes to fill in edges on electric current sample

Sampling for Big Data HT Estimators for Graphs ◊ Tin can construct HT estimators from uniform vertex samples [Frank 78] – Evaluate the desired function on the sampled graph (eastward. g. boilerplate degree) ◊ For functions of edges (e. g. number of edges satisfying a property): – Scale up accordingly, by N(N-i)/(k(k-i)) for sample size k on graph size N – Variance of estimates can also be bounded in terms of Due north and k ◊ Similar for functions of three edges (triangles) and higher: – Scale up by NC iii/k. C iii ≈ 1/p 3 to become unbiased estimator – High variance, then other sampling schemes have been adult

Sampling for Large Data Graph Sampling Heuristics "Heuristics", since few formal statistical backdrop are known ◊ Breadth first sampling: sample a node, and so its neighbours… – Biased towards high-degree nodes (more chances to attain them) ◊ Snowball sampling: generalize BF past picking many initial nodes – Respondent-driven sampling: weight the snowball sample to requite statistically sound estimates [Salganik Heckathorn 04] ◊ Forest-burn down sampling: generalize BF by picking only a fraction of neighbours to explore [Leskovec Kleinberg Faloutsos 05] – With probability p, motility to a new node and "kill" electric current node No "i true graph sampling method" – Experiments bear witness different preferences, depending on graph and metric [Leskovec, Faloutsos 06; Hasan, Ahmed, Neville, Kompella xiii] – None of these methods are "streaming friendly": require static graph □ Hack: apply them to the stream of edges as-is

Sampling for Big Data Random Walks Sampling ◊ Random walks have proven very effective for many graph computations – Page. Rank for node importance, and many variations ◊ Random walk a natural model for sampling a node – – – Perform "long enough" random walk to selection a node How long is "long enough" (for mixing of RW)? Can get "stuck" in a subgraph if graph not well-continued Costly to perform multiple random walks Highly non-streaming friendly, only suits graph crawling ◊ Multidimensional Random Walks [Ribeiro, Towsley ten] – – Selection grand random nodes to initialize the sample Pick a random border from the union of edges incident on the sample Can be viewed as a walk on a high-dimensional extension of the graph Outperforms running k independent random walks

Sampling for Big Data Subgraph estimation: counting triangles ◊ Hot topic: sample-based triangle counting – Triangles: simplest non-trivial representation of node clustering □ Regard as prototype for more complex subgraphs of involvement – Measure of "clustering coefficient" in graph, parameter in graph models… ◊ Uniform sampling performs poorly: – Run a risk that randomly sampled edges happen to grade subgraph is ≈ 0 ◊ Bias the sampling so that desired subgraph is preferentially sampled

Sampling for Big Information Subgraph Sampling in Streams Want to sample one of the T triangles in a graph ◊ [Buriol et al 06]: sample an edge uniformly, then pick a node – Scan for the edges that consummate the triangle – Probability of sampling a triangle is T/(|East| (|V|-2)) ◊ [Pavan et al 13]: sample an border, then sample an incident border – Scan for the edge that completes the triangle – (After bias correction) probability of sampling a triangle is T/(|E| ) □ = max caste, considerably smaller than |5| in well-nigh graphs ◊ [Jha et. al. KDD 2013]: sample edges, the sample pairs of incident edges – Scan for edges that complete "wedges" (edge pairs incident on a vertex) ◊ Advert: Graph Sample and Hold [Ahmed, Duffield, Neville, Kompella, KDD 2014] – General framework for subgraph counting; eastward. m. triangle counting

Sampling for Large Data Graph Sampling Summary ◊ Sampling a representative graph from a massive graph is difficult! ◊ Current state of the art: – Sample nodes/edges uniformly from a stream – Heuristic sampling from static/streaming graph ◊ Sampling enables subgraph sampling/counting – Much effort devoted to triangles (smallest non-piffling subgraph) ◊ "Real" graphs are richer – Different node and edge types, attributes on both – Just scratching surface of sampling realistic graphs

Sampling for Big Data Current Directions in Sampling

Sampling for Big Data Outline ◊ Motivating application: sampling in big Isp networks ◊ Basics of sampling: concepts and estimation ◊ Stream sampling: uniform and weighted instance – Variations: Concise sampling, sample and hold, sketch guided BREAK ◊ Advanced stream sampling: sampling as price optimization – Var. Opt, priority, construction aware, and stable sampling ◊ Hashing and coordination – Bottom-thousand, consistent sampling and sketch-based sampling ◊ Graph sampling – Node, edge and subgraph sampling ◊ Conclusion and futurity directions

Sampling for Big Data Role and Challenges for Sampling ◊ Matching – Sampling mediates between data characteristics and analysis needs – Instance: sample from power-constabulary distribution of bytes per menstruation… □ just besides make accurate estimates from samples □ simple uniform sampling misses the large flows ◊ Residuum – Weighted sampling across central-functions: due east. k. customers, network paths, geolocations □ encompass minor customers, not merely big □ cover all network elements, not only highly utilized ◊ Consistency – Sample all views of same event, period, customer, network element □ across unlike datasets, at unlike times □ independent sampling small intersection of views

Sampling for Large Data Sampling and Big Data Systems ◊ Sampling is still a useful tool in cluster computing – Reduce the latency of experimental analysis and algorithm design ◊ Sampling equally an operator is piece of cake to implement in Map. Reduce – For compatible or weighted sampling of tuples ◊ Graph computations are a cadre motivator of big data – Page. Rank equally a canonical big ciphering – Graph-specific systems emerging (Pregel, LFgraph, Graphlab, Giraph…) – But… sampling primitives not nonetheless prevalent in evolving graph systems ◊ When to do the sampling? – Option ane: Sample every bit an initial step in the computation □ Fold sample into the initial "Map" footstep – Option two: Sample to create a stored sample graph before computation □ Allows more complex sampling, e. thou. random walk sampling

Sampling for Big Data Sampling + KDD ◊ The coaction betwixt sampling and information mining is not well understood – Demand an understanding of how ML/DM algorithms are affected by sampling – E. g. how large a sample is needed to build an accurate classifier? – E. g. what sampling strategy optimizes cluster quality ◊ Expect results to be method specific – I. east. "IPPS + chiliad-ways" rather than "sample + cluster"

Sampling for Big Data Sampling and Privacy ◊ Current focus on privacy-preserving data mining – Evangelize promise of big data without sacrificing privacy? – Opportunity for sampling to be part of the solution ◊ Naïve sampling provides "privacy in expectation" – Your data remains individual if yous aren't included in the sample… ◊ Intuition: uncertainty introduced past sampling contributes to privacy – This intuition tin be formalized with different privacy models ◊ Sampling tin be analyzed in the context of differential privacy – Sampling lonely does not provide differential privacy – Merely applying a DP method to sampled data does guarantee privacy – A tradeoff between sampling rate and privacy parameters □ Sometimes, lower sampling rate improves overall accurateness

Sampling for Big Data Advert: Now Hiring… ◊ Nick Duffield, Texas A&M – Phds in large information, graph sampling ◊ Graham Cormode, University of Warwick Britain – Phds in large data summarization (graphs and matrices, funded by MSR) – Postdocs in privacy and data modeling (funded by EC, AT&T)

x 10 10 9 10 8 x vii 10 6 x 5 x iv x 3 x ii x 1 x' 10 10' 9 ten' 8 x' 6 ten' 5 x' iv 10' iii ten' 2 ten' 1 0 00 i 01 xi 000 001 010 011 100 101 110 111 Sampling for Large Information Graham Cormode, University of Warwick G. [email protected] ac. united kingdom Nick Duffield, Texas A&Grand University [email protected] edu 10

9 X 8 X 7,

Source: https://slidetodoc.com/x-10-x-9-x-8-x-7-2/

Posted by: sheltonposeveropme.blogspot.com

Share this post